As retail leaders, our world is full of choices for which there is not one clear answer.  Accountants operate under the straight forward rules of math.  Engineers operate under the clear logic of physics.  Even attorneys operate under the documented rules of law.  In contrast, as retailers, we make decisions every day that are based on the uncertain nature of human beings.  If we try too hard to find certainty, we end up paralyzed and unable to make decisions at all.  If we fail to analyze situations enough, we end up making decisions without proper consideration of all that we should consider.  So how can we find an effective “formula” for decision making that accepts the impossibility of certainty AND gives us robust objectivity?

One solution is to use probabilistic thinking.  This means envisioning the value of various possible outcomes, assigning probabilities to each possible outcome, and doing the math to determine an expected value for each potential choice.  Comparing the expected values of various options gives us a probabilistic perspective on which choice to make.

Consider the example of one of those tough decisions we often must make.  We have an open supervisory position on the team, and we must choose from three candidates.  One possible choice is to promote a long term salesperson who has paid his dues.  Another choice is to promote a young, up and coming salesperson who shows lots of promise but hasn’t yet acquired the level of experience of the long term employee.  And the third possible choice is to hire an external candidate who already has supervisory experience but would be more of an unknown gamble.  As you are reading this, your mind is probably filling with all of the pros and cons of each option.  You are probably also beginning to argue with yourself about which of the pros and cons are most important to focus on.  If you were really in the situation, your mind would also be filling with assessments of the three candidates and how their specific characteristics match up to the pros and cons.  That’s a lot for the conscious brain to sift through, and without more structure, you will probably go round and round, floundering in the uncertainty of it all.

A probabilistic approach will give more structure to the analysis of the options.  Let’s take four steps as follows:

• List all of the criteria that we should consider about the candidates for this decision.  In real life, there are probably dozens of criteria to be considered for this type of decision.  To keep things simple for this example, we are going to use just three… ability to coach people, ability to sell, and ability to fit into the existing culture.
• Weight the criteria in terms of importance and relevance.  In this case, we want to weight the criteria based on how important each will be to the chosen candidate’s success in the role.  You can use whatever weighting scale you wish; for this example, we will weight from 1 to 10, with 10 being the most important.  Ability to coach people will be a 9 (since that’s the primary objective of the role), ability to sell will be a 3 (since this is a supervisory position), and fit into the existing culture will be a 4 (since some culture change may actually be refreshing).
• Determine the probability that each option will fulfill each criterion.  In this case, we will determine the probability that each candidate will be successful in coaching employees, selling, and fitting into the culture.  We can create a chart like the following:
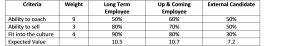
• Do the math to calculate the expected value of each possible choice.  In this case, for the long term employee, we multiply 50% x 9, 80% x 3, and 90% x 4, and then we add those three products together to get 10.5.  When we do the same thing for the up and coming employee, we get 10.7, and when we do the same for the external candidate, we get 7.2.

So, the expected value of promoting the up and coming employee is higher than the other two options, though promotion of the long term employee is a close second.  Does this mean that choice will definitely work out best?  No, not at all.  Remember that we can’t eliminate uncertainty.  All we can do is give ourselves an objective way to analyze the uncertainty we know exists.  The expected value difference in this example depends largely on our assessment that the up and coming employee has a better chance of being an effective coach than the long term employee.  But, we still have only assigned a 60% probability to that result.  This process does give us an objective way to analyze our assumptions.  With a sharper focus on the one major defining difference, we can dig a bit deeper on that issue with our candidates and test our assumption more fully.  Perhaps that will lead to a change in our assessments, or it may further solidify our beliefs.  Either way, we will have used probabilistic thinking to improve our decision making process, and we will have pulled ourselves out of the endless circle of debating within a world of ambiguity.